Adam Łomnicki
Wprowadzenie do statystyki dla przyrodników
Wydanie piąte poprawione
Wydawnictwo Naukowe PWN, Warszawa
2014
Spis
rzeczy
1.
Prośba autora do
czytelników
2.
Errata do wydania piątego
2a. Errata do wydania czwartego
4. R: język i statystyczne oprogramowanie
Prośba autora do czytelników
Dotychczasowe wydania „Wprowadzenia do statystyki dla
przyrodników” nauczyły mnie, że różnego rodzaju błędy, od drobnych błędów
liczbowych do różnego rodzaju niejasności w tekście, są nie do uniknięcia.
Dlatego bardzo proszę wszystkich czytelników, a szczególnie studentów, mających
po raz pierwszy styczność z tą książką o zawiadomienie mnie o wszelkich napotkanych błędach,
niejasnościach i sprzecznościach, które napotkają. Pozwoli to na uzupełnienie Erraty na niniejszych stronach www i stałe
ulepszanie tekstu. Przyjmę też wszelkie uwagi krytyczne o tej książce. Aby nie
ograniczać czytelników w krytyce sugeruję, aby e-maile do mnie przesyłać
anonimowo, posłując się adresem e-mailowym bez nazwiska.
Ze swej strony będę się starał, aby dane do niektórych przykładów
ćwiczeń podać w Excelu (Wybrane Dane), co
pozwoli czytelnikom przeliczyć je używając podanego poniżej oprogramowania R
lub swoim własnym programem statystycznym, bez ich żmudnego przepisywania.
Do rozdziału 15. o analizie kowariancji nie było sensu podawania
dodatkowych danych liczbowych dla ćwiczeń, oprócz tych użytych w przykładzie.
Obliczenia w tej technice statystycznej dokonywane są za pomocą odpowiednich
programów i dlatego nie ma potrzeby ćwiczyć czytelnika w umiejętności
stosowania właściwych wzorów. Czytelnik może natomiast sprawdzić przykład tam
omawiany w swym programie statystycznym i dlatego w Excelu podano jeszcze raz
jego dane liczbowe (Tabela 15.1 w pliku Wybrane-Dane). W analizie kowariancji ważne jest
natomiast zrozumienie, jakimi wartościami się posługujemy i jaki jest ich
związek z danymi empirycznymi. Takie zrozumienie powinno być uzyskane przez
wykonanie Ćwiczenia 15.1.
Do niniejszej witryny dodano bardzo prosty podręcznik języka
i oprogramowania R, związany że wstępnymi
rozdziałami czwartego wydania „Wprowadzenia...” Podręcznik ten będzie w
przyszłości poprawiany i uzupełniamy, pod warunkiem uzyskania reakcji od
czytelników, czy jest on pożyteczny i czy dalsze opracowanie jego jest
sensowne.
Errata do wydania piątego
na dzień 28 lipca 2014
Strona 78, wiersz 6 od góry, zamiast p daj
μ
 Errata do wydania
czwartego
Errata do wydania
czwartego
na dzień 24 maja 2014
Strona 76, rycina 5.2, w opisie przy osi poziomej,
druga pozycja od lewej strony zamiast -3σ daj -2σ
Strona 76, w opisie ryciny 5.2, wiersz 1, zamiast n daj
μ
Strona 94, wiersz 6 od dołu, zamiast p = daj
μ =
Strona 108, wiersz 8 od góry, zamiast d = daj D =
Strona 108, wiersz 10 od góry, zamiast d = daj
D =
Strona 108, wiersz 15 od góry, zamiast d = daj
D =
Strona 108, wiersz 12 od
dołu, zamiast ![]() = daj
= daj ![]() =
=
Strona 108, wiersz 7 od dołu, zmień wzór (7.1) na
wzór ![]()
Strona 109, wiersz 8 od góry, zamiast d = daj D =
Strona 109, wiersz 9 od góry, zamiast d daj D oraz zamiast ![]() daj
daj ![]()
Strona 109, wiersz 10 od góry, zamiast d daj D i zamiast ![]() daj
daj ![]()
Strona 109, wiersz 14 od dołu, zamiast ∑d = daj ∑D =
Strona 109, wiersz 13 od dołu, zamiast ∑![]() = daj ∑
= daj ∑![]() =
=
Strona 109, wiersz 11 od dołu, zamiast ![]() daj
daj ![]()
Strona 109, wiersz 8 od dołu, zamiast ![]() daj
daj ![]()
Strona 109,
wiersz 5 od dołu, zamiast ![]() daj
daj ![]()
Strona 109, wiersz 3 od dołu, zamiast ![]() daj
daj ![]()
Strona 109,
wiersz 1 od dołu, zamiast ![]() daj
daj ![]()
Strona 110, wiersz 14 od góry, zamiast d daj D
Strona 112, wiersz 8 i 9 od góry, zamiast statystyki t dla różnic między średnimi obliczamy z wzoru
 (7.5)
(7.5)
daj tekst statystykę t otrzymujemy porównując absolutną wartość różnicy między średnimi dla obu prób z hipotezą zerową i dzieląc tę wartość przez błąd standardowy tej różnicy, a mianowicie
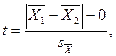 (7.5)
(7.5)
Strona 112, wiersze 7 do 4 od dołu, zamiast tekstu a nie można założyć jednorodności wariancji, wówczas liczbę stopni swobody nie trzeba obliczać jako średniej ważonej, jest ona natomiast dwukrotnie mniejsza i wynosi
df = N – 1. (7.6)
daj tekst wówczas liczba stopni swobody wynosi
df = 2N – 2. (7.6)
Strona 113, wiersz 10 od góry, zamiast 52,1 daj 52,11
Strona 113, wiersz 11 od dołu, zamiast 51,11 daj 52,11
Strona 115,
wiersz 6 od góry, wzór (7.7), lewa strona: zamiast ![]() daj
daj ![]()
Strona 115, wiersz 11 od góry, zamiast (7.5) daj (7.7)
Strona 115, wiersz 14 od góry, zamiast (7.5) daj (7.7)
Strona 115,
wiersz 15 od góry, lewa strona: zamiast ![]() daj
daj ![]()
Strona 116,
wiersz 6 od dołu, zamiast d daj D
Strona 126,
wiersz 14 od góry, zamiast bo daj to
Strona 136,
wiersz 2 od góry, prawa strona równania: zamiast ![]() daj
daj ![]()
Strona 150, wiersz 9 od góry: po
prawej stronie równania ostatnia różnica w nawiasie podniesiona do kwadratu
zamiast![]() , powinno być
, powinno być ![]()
Strona 234. wiersz 7 od dołu. Po tekście gdy N > 10. daj: Gdy jest tu napisane, że rs powinno być większe od wartości krytycznej oznacza to że absolutna wartość rs winna być większa od krytycznej. Gdybyśmy otrzymali rs = -0,902, przy N =6, to ponieważ absolutna wartość rs = 0,902, należy uznać tę korelację za istotną z P < 0,05.
Strona 238, rycina 14.11, w dolnej części dolnego wykresu zamiast litery R powinna być litera B
Strona 241,
wiersz 3 i 2 od dołu. Zdanie: Ważne jest tylko, aby ten wymiar X był skorelowany z masą ciała Y.
usuń
Strona
249, tabela 15.3, pozostaw opis tej
tabeli, ale zmień ją tak jak przedstawiono poniżej
__________________________________________________________________________________ Źródła SSKO df średni F P
zmienności kwadrat
![]() Ogólna(SP) 38,772 10
Ogólna(SP) 38,772 10
Między
grupami(SM) 28,485 1 28,485 24,920
< 0,001
W grupach (SC) 10,287 9 1,143
Strona 250, tabela 15.4, pozostaw opis tej tabeli, ale zmień ją tak jak przedstawiono poniżej
__________________________________________________________________________________
Źródła SSKO df średni
F P
zmienności kwadrat
![]() Ogólna (SC) 10,287 9
Ogólna (SC) 10,287 9
Między
grupami(SG) 3,410 1 3,410 3,967
> 0,05
W grupach (SW) 6,877 8
0,860
Strona 251, wiersze 3 do 1 od dołu: zamiast części zdania należy zrezygnować z poszukiwania różnic miedzy średnimi w grupach i ograniczyć się do badania różnic w nachyleniu prostych regresji daj nie ma uniwersalnej odpowiedzi na pytanie, jaka jest różnica między grupami, bo różnica ta zależy od tego, dla jakiej wartości zmiennej towarzyszącej jest oceniana. Analiza takich przypadków jest skomplikowana i przekracza ramy tego podręcznika.
Strona 259, wiersz 2 od dołu, zamiast (e) 0,00668 daj (e) 0,0668
![]()
Ćwiczenie 15.1
Ćwiczenie to opiera się na
danych i wykresach przedstawionych w rozdziale 15. Polega ono na tym, aby na
wykresach naszkicować wszystkie używane w analizie kowariancji odchylenia i kwadraty
odchyleń. Obejmuje ono dwie części: (15.1a) dotyczące różnic miedzy grupami
i (15.1b) jednorodności prostych regresji. Dla każdej z tych części należy
pobrać stronę z wykresami (Wykres-a i Wykres-b) wydrukować ją, naszkicować na tych
wykresach odpowiednie odchylenia, a następnie przy każdym odchyleniu
naszkicować jego kwadrat tak jak to zrobiono na ryc. 14.4 (strona 217).
Kierunek szkicowania tego kwadratu jest bez znaczenia, natomiast użycia dwóch
kolorów różnych dla każdej grupy czyni szkic nieco czytelniejszym. Sprawdzenia
czy szkice zostały wykonane poprawnie można dokonać porównując je z wynikami
dla samych odchyleń (W1-a i W1-b)
oraz dla kwadratów odchyleń (W2-a i W2-b).P
