Przykładowe pytania z ćwiczeń i egzaminu

1. Zaokrąglij liczby do jednej dziesiętnej:

4,35 28,25

17,249 17,39

17,2009 12,2501

0,1445 2,1445

34,95 0,97

2. W pewnym gnieździe sikory modrej było 9 samic i 6 samców

1. Jaka była proporcja samców?

2. Jaki to procent?

3. Jaki był stosunek liczby ♀ do ♂?

4. A stosunek liczby ♂ do ♀?

3. Badano 10 gniazd sikory bogatki i stwierdzono następujące liczby piskląt opuszczających

gniazdo (wylotów):

9, 0, 1, 4, 4, 4, 9, 16, 1, 4.

1. Dla tego szeregu oblicz średnią arytmetyczną, medianę, wartość modalną. Przedstaw ten szereg graficznie zaznaczając na nim te trzy miary tendencji centralnej.

2. Dokonaj transformacji powyższego szeregu przez pierwiastkowanie i tak transformowany szereg także przedstaw graficznie.

3. Dla danych transformowanych oblicz średnią arytmetyczną. Dokonaj transformacji danych w odwrotnym kierunku i porównaj ja ze średnią z danych oryginalnych. Dodaj komentarz.

4. W jakiej skali podane są liczby wylotów?

4. Czy można zamienić pomiary w skali:

1. interwałowej na nominalna dychotomiczną?

2. nominalnej na porządkową?

3. nominalnej na interwałową?

4. interwałowej na porządkową?

5. Trzech różnych ornitologów przeprowadziło obserwacje odpowiednio 8, 10 i 13 gniazd

sikory bogatki w różnych oddziałach tego samego lasu w celu określenia liczby piskląt

opuszczających gniazdo. Otrzymali następujące wyniki:

1-szy: 1, 4, 0, 7, 5, 12, 10, 6;

2-gi: 11, 2, 5, 3, 0, 9, 7, 13, 10, 6;

3-ci: 10, 8, 3, 0, 7, 12, 4, 9, 11, 8, 6, 2, 10.

Oblicz średnią liczbę podlotów dla każdej próby oddzielnie, a następnie dla wszystkich pomiarów. Podaj, której średniej użyjesz dla tych obliczeń.

6. W 6 kolejnych latach mierzono współczynnik reprodukcji netto (R) jednego z gatunków modraszków żyjących na podkrakowskich łąkach i uzyskano następujące współczynniki:

2, 1, 1/2, 8, 1/4, 1/2.

Podaj nazwę średniej, którą tu zastosujesz, oblicz tę średnią i medianę.

Czy wielkość populacji zmieniła się po 6-ciu latach?

7. Co dzieje się ze średnią z próby z populacji generalnej jeżeli zwiększamy liczbę pomiarów:

1. rośnie

2. maleje

3. jest obciążonym estymatorem

4. zbliża się do średniej dla populacji generalnej

8. Rozkład długości obwodu bicepsa studentów polonistyki

1. Jak nazwa się powyższy sposób przedstawienia pomiarów?

2. Czego brak na osi X?

3. Podaj środek i granice rzeczywiste pierwszego przedziału

4. Z jaką dokładnością mierzono bicepsy?

Na powyższym wykresie na osi Y mamy:

a) rozkład obwodu bicepsa dłuższy od liczby wyznaczającej początek przedziału,

b) liczebność pomiarów w danym przedziale,

c) proporcje obwodu bicepsa dłuższe od liczby wyznaczającej początek przedziału,

d) częstość pomiarów w danym przedziale.

Gdybyśmy zlogarytmowali wartości wszystkich pomiarów, to będzie to:

a) rozszerzanie, c) transformacja,

b) zwężanie, d) kodowanie.

9. Obwody bicepsów [cm]:

26 23 20 19 23 38 28 34 28 23 27

1. Podaj jaki jest zakres pomiarów.

2. Oblicz średnią.

3. Zakoduj dane odejmując średnią. Oblicz średnią dla danych zakodowanych. Odkoduj ją.

4. Transformuj dane podnosząc je do drugiej potęgi. Oblicz średnią i odkoduj ją.

10. W pewnej publikacji naukowej przedstawiono wyniki badań mających na celu sprawdzenie, czy samce i samice pewnego gatunku biegacza różnią się ciężarem ciała.

Analizy oparto na pomiarach 10 samców i 10 samic i przeprowadzono je przy użyciu testu t-Studenta dla par wiązanych.

W publikacji zaprezentowano następujący wynik analiz: t=4,11, df=20, p<0,10. Na podstawie analiz wyciągnięto wniosek o braku różnic między płciami.

Przyjmując hipotezę zerową popełniono jednak błądy. Uzasadnij dlaczego.

11. W 5 gniazdach sikory bogatki znaleziono następujące liczby larw muchówek:

16 8 12 2 7

Oblicz dla tego szeregu statystycznego:

a) średnią arytmetyczną

b) wariancję

c) odchylenie standardowe

Sumę kwadratów odchyleń oblicz dwoma sposobami.

12. Pewien ornitolog odłowił i zważył po 6 osobników kruka i kosa, uzyskując następujące wyniki:

Kruk: 1301, 1248, 1281, 1219, 1270, 1269 [g]

Kos: 59, 61, 58, 60, 58, 59 [g]

a) Oblicz średnią arytmetyczną, wariancję i odchylenie standardowe dla obu serii pomiarów.

b) Czy można określić różnice w zmienności pomiarów między tymi dwoma próbami, a jeżeli tak, w jaki sposób?

13. Naszkicuj na jednym wykresie krzywe dwóch hipotetycznych rozkładów normalnych

a) O dużej średniej i dużym odchyleniu standardowym.

b) O małej średniej i małym odchyleniu standardowym.

14. Zarobki 8 osób będących pracownikami firmy „Kasztanowcowiaczek & S-ka” wynosiły:

1,5; 1,5; 1,5; 2,0; 3,0; 3,0; 5,0; 10,0 (tys. zł.)

Oblicz: modalną, medianę i średnią

15. Naszkicuj na jednym wykresie krzywe dwóch hipotetycznych rozkładów normalnych

c) O dużej średniej i dużym odchyleniu standardowym.

d) O małej średniej i małym odchyleniu standardowym.

16. Badano występowanie pasożytniczych nicieni w przewodach pokarmowych samców i samic pewnego gatunku ryb.

Aby sprawdzić, czy istnieje zależność między płcią a występowaniem nicieni pobrano odpowiednią próbę i przeprowadzono test chi kwadrat. Podaj:

a) nazwę skali z jaką mamy do czynienia w tym teście

b) hipotezę zerową

c) wartość krytyczną przy założeniu poziomu istotności 0,05

Jeśli z obliczeń wynika wartość statystyki testu 5,612, podaj:

d) swoją decyzję o przyjęciu lub odrzuceniu hipotezy zerowej

e) błąd I rodzaju

17. Badano sukces lęgowy kosów w Lesie Wolskim. Okazało się, że spośród 200 gniazd, lęgi skończyły się sukcesem w 120 gniazdach. Oblicz 95% przedział ufności dla proporcji gniazd z sukcesem lęgowym.

18. Pewien student leśnictwa mierzył długości szyszek świerku w Puszczy Knyszyńskiej.

W próbie 25 szyszek średnia długość wynosiła 9 cm, a odchylenie standardowe 1,5 cm.

a) Co można powiedzieć o średniej długości szyszek świerkowych w całej Puszczy Knyszyńskiej?

b) Jakie założenia muszą być spełnione?

19. Pewien pszczelarz obserwował liczbę robotnic powracających do ula z pyłkiem przy 9 ulach swojej pasieki i notował ich liczbę (I) w ciągu 5 minut. Następnie dodał syropu cukrowego do podkarmiaczki każdego ula i powtórnie zanotował liczbę (II) robotnic wracających z pyłkiem w ciągu 5 minut. Otrzymał następujące wyniki:

I: 12 5 24 11 37 10 24 18 6

II: 15 4 26 13 40 8 30 22 7

Czy dodanie syropu do podkarmiaczek wpłynęło na liczbę robotnic latających po pożytek?

20. Pewien student obserwował intensywność karmienia piskląt przez kosy rano (R) od 7:00 do 8:00 i po południu (P) od 16:00 do 17:00 w tych samych 9 gniazdach. Otrzymał on następujące liczby przylotów rodziców z pokarmem:

R: 15 14 28 20 40 11 30 22 13

P: 12 13 24 21 37 10 24 18 12

Sprawdź, czy intensywność karmienia piskląt zależy od pory dnia? Przeprowadź wszystkie etapy testowania hipotez.

21. Badano długość liści buka. Kiedy należy zastosować pary wiązane, a kiedy próby niezależne, aby odpowiedzieć na następujące pytania:

a) Czy długość liści jest różna w Puszczy Niepołomickiej i w Puszczy Boreckiej?

b) Czy liście zebranie z drzew różnią się od liści zebranych spod drzew?

c) Czy liście rosnące od strony wschodniej różnią się od liści rosnących po stronie zachodniej?

d) Czy długość liści w sezonie 2002 i 2003 różni się od siebie jeżeli leśnictwo wyraziło zgodę na znakowanie drzew?

e) Czy długość liści w sezonie 2002 i 2003 różni się od siebie jeżeli drzewa nie były znakowane?

Podaj po kilka własnych przykładów badań z zastosowaniem prób niezależnych i par wiązanych.

22. Badano liczbę furażerek mrówki rudnicy wracających do gniazda z pokarmem na 10 mrowiskach rano i wieczorem. Otrzymano następujące wyniki:

Rano: 8 10 10 11 13 7 6 8 9 14

Wieczorem: 6 9 8 9 8 13 10 12 7 7

Czy liczba furażerek wracających do gniazda z pokarmem różni się między porami dnia?

Podaj: nazwę testu, statystyki, decyzję i błąd I rodzaju.

23. Aby sprawdzić, czy masa urodzeniowa noworodków jest związana z wiekiem matki przeprowadzono analizę korelacji wykorzystując dane dotyczące 100 kobiet.

W wyniku obliczeń uzyskano r=0,15. Podaj:

a) nazwę skali, w której wyrażone są dane o wieku kobiet

b) hipotezę zerową

c) założenia testu istotności korelacji

d) liczbę stopni swobody

e) wartość odpowiedniej statystyki

f) decyzję odnośnie tych badań

24. Wykorzystując dane o tempie wzrostu koloni bakterii w różnych temperaturach ustawianych na termostatach przeprowadzono analizę

regresji uzyskując współczynnik nachylenia prostej regresji równy 0,2 i wyraz wolny równy –0,9. Podaj:

a) równanie tej regresji

b) wartość tempa wzrostu bakterii w temperaturze +20˚C

c) który model regresji należałoby zastosować

d) jakie założenia dotyczące rozkładów obu zmiennych należałoby poczynić

25. Podaj znane Ci różnice między odchyleniem standardowym a błędem standardowym. Jak zmieniają się te statystyki wraz ze wzrostem wielkości próby?

26. Pewien rolnik mający w planach założenie hodowli krów mlecznych postanowił sam sprawdzić na niewielkich stadach mleczność dwóch ras krów. W grupie 16 krów czerwono-białych (RW) i 25 czarno-białych (BW) hodowanych w identycznych warunkach, z jednego udoju otrzymał następujące średnie objętości mleka w przeliczeniu na jedną krowę:

RW – 14,7 L mleka (SD = 1,4 L)

BW – 15,3 L mleka (SD = 1,5 L)

Przedstaw graficznie w jakich granicach z 95% prawdopodobieństwem znajdują się średnie z populacji RW i BW. Wysnuj wnioski statystyczne i powiedz jakiej rady udzieliłbyś temu rolnikowi przy zakupie stada krów mlecznych.

27. Zważono 61 chomików, a ponieważ ich ciężary (w gramach) były nieco dodatnio skośne dokonano transformacji przez spierwiastkowanie pierwiastkiem kwadratowym, uzyskując dla tak transformowanych danych średnią 20,0 i błąd standardowy 0,5. Oblicz 95% przedział ufności oraz średnią i granice przedziału ufności dla danych nietransformowanych.

28. Po przeprowadzeniu dwustronnego testu t-Studenta uzyskano błąd I rodzaju p=0,001. Co możemy powiedzieć na temat wartości t uzyskanej w tym teście?

29. Na 7 powierzchniach w Pieninach odławiano chrząszcze z rzędu kózkowatych i dla każdej z powierzchni stwierdzono następujące liczby gatunków:
12, 4, 8, 6, 2, 10, 6.

Oblicz średnią liczbę gatunków przypadających na 1 powierzchnię, wariancję, odchylenie standardowe i medianę.

30 Pewien entomolog badał występowanie rzadkiego motyla z gatunku Niepylak apollo na kilku łąkach w Pieninach.

Otrzymał następujące liczebności na każdej łące: 9, 25, 1, 9, 9.

Stransformuj te dane przez pierwiastkowanie (pierwiastek kwadratowy) i oblicz na danych transformowanych:

a) średnią arytmetyczną

b) wariancję

c) odchylenie standardowe

d) współczynnik zmienności

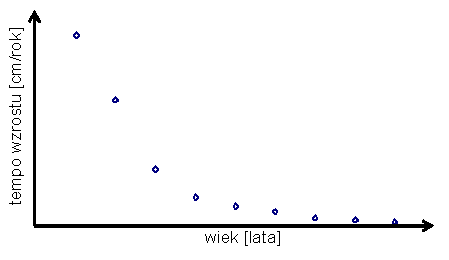
31. Wykres przedstawia zależność tempa wzrostu człowieka od jego wieku. Jak należy postąpić z takimi danymi, aby ustalić istotność związku między tymi dwoma cechami?

32. Badano zawartość cynku w organizmie biegacza Pterostichus versicolor, z pomocą spektofotometru. Za pomocą roztworów o znanych stężeniach (c_Zn) wykalibrowano spektofotometr otrzymując następujące wartości absorbancji (A):

cZn [mg/L]	0	0,2	0,5	1,0	2,0
A	0,002	0,035	0,094	0,161	0,311

a) Narysuj wykres punktowy zależności absorbancji od stężenia roztworu Zn.

b) Jedno z niżej podanych równań opisuje tą zależność. Które?

A = 0,153 – 0,007 c_Zn A = 0,002 – 0,153 c_Zn

A = 0,007 + 0,153 c_Zn A = 0,153 + 0,007 c_Zn

c) Jak nazywa się ta prosta? Nanieś ją na wykres.

d) Jakie jest stężenie cynku w próbce z osobnika nr. 90, jeżeli absorbancja wynosi 0,110?

e) Czy jest to model I czy II szeregu dwucechowego?

33. Badając na przestrzeni 20 lat związek między średnią temperaturą powietrza w marcu, a średnią datą przystąpienia do lęgów sikory modrej uzyskano r = 0,60. Oblicz, czy siła tego związku jest istotna. Podaj błąd I rodzaju, nawet, jeżeli go nie popełniasz. Z którym modelem szeregu dwucechowego mamy tu do czynienia?

34. Pewien badacz chciał sprawdzić, czy proporcja płci u żółwia błotnego odbiega od przewidywanego 0,5. Pobierając próbę 15 osobników uzyskał 5 samców i 10 samic.

Aby sprawdzić, na ile uzyskany wynik jest dziełem przypadku przeprowadził odpowiedni test statystyczny, w którym wartości krytyczne wyrażone są w postaci liczby sukcesów. Podaj:

a) nazwę rozkładu z którego ten test korzysta

b) określ parametry tego rozkładu.

c) wartości krytyczne dla tego testu

d) decyzję odnosnie tego testu

35. Kojarząc heterozygotę z homozygotą recesywną u groszku, pewien badacz przewidywał, że w potomstwie uzyska połowę kwiatów czerwonych i połowę białych.

Pobierając próbę 20 osobników potomnych uzyskał jednak 7 osobników białych i 13 czerwonych. Aby sprawdzić, na ile uzyskany wynik jest dziełem przypadku przeprowadził odpowiedni test statystyczny, w którym wartości krytyczne wyrażone są

w postaci liczby sukcesów. Podaj:

a) nazwę rozkładu z którego ten test korzysta.

b) określ parametry tego rozkładu

c) podaj wartości krytyczne dla tego testu

d) decyzję odnosnie tego testu